IEEE VIS 2024 Content: Gridlines Mitigate Sine Illusion in Line Charts

Gridlines Mitigate Sine Illusion in Line Charts



 Clayton J Knittel - Google LLC, San Francisco, United States

 Jane Awuah - Georgia Institute of Technology, Atlanta, United States

 Steven L Franconeri - Northwestern University, Evanston, United States

Cindy Xiong Bearfield - Georgia Tech, Atlanta, United States

 Screen-reader Accessible PDF

 Download Supplemental Material

 Room: Bayshore VI

2024-10-17T13:33:00ZGMT-0600Change your timezone on the schedule page
2024-10-17T13:33:00Z

Exemplar figure, described by caption below — Looking at this visualization of two lines depicting the revenue of two products over time. Product A is consistently doing better than Product B, and thus have higher revenue throughout time. Both products' revenue are growing, with their line slopes increasing over time. Your task it to compare whether the difference between their revenue, or the deltas between the two lines, are bigger at an earlier time (Time 1), or a later time (Time 2). While it may be tempting to say the difference is bigger at Time 1, the correct answer is Time 2. This is a visual illusion commonly referred to as the sine illusion. It is an underestimation of the difference between two lines when both lines have increasing slopes.

Fast forward

Full Video

Keywords

sine illusion, gridlines, perception, bias, thresholds

Abstract

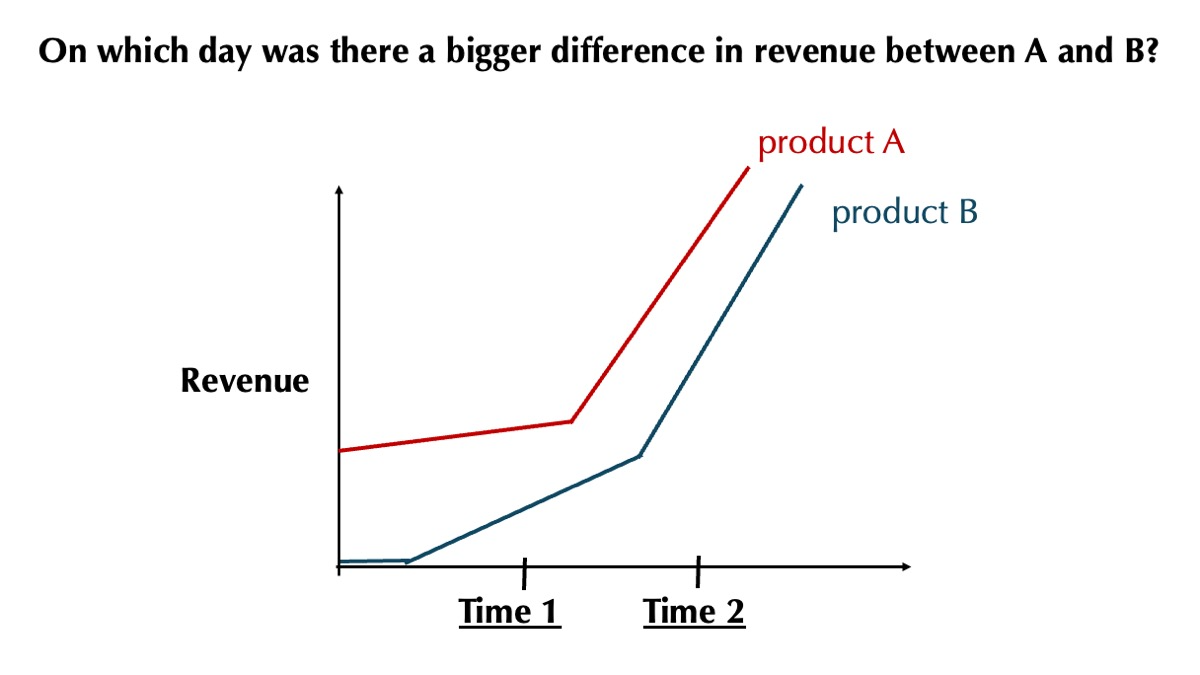
Sine illusion happens when the more quickly changing pairs of lines lead to bigger underestimates of the delta between them.We evaluate three visual manipulations on mitigating sine illusions: dotted lines, aligned gridlines, and offset gridlines via a user study. We asked participants to compare the deltas between two lines at two time points and found aligned gridlines to be the most effective in mitigating sine illusions.Using data from the user study, we produced a model that predicts the impact of the sine illusion in line charts by accounting for the ratio of the vertical distance between the two points of comparison. When the ratio is less than 50\%, participants begin to be influenced by the sine illusion. This effect can be significantly exacerbated when the difference between the two deltas falls under 30\%.We compared two explanations for the sine illusion based on our data: either participants were mistakenly using the perpendicular distance between the two lines to make their comparison (the perpendicular explanation), or they incorrectly relied on the length of the line segment perpendicular to the angle bisector of the bottom and top lines (the equal triangle explanation). We found the equal triangle explanation to be the more predictive model explaining participant behaviors.