A Practical Solver for Scalar Data Topological Simplification

Fast forward

Full Video

Keywords

Topological Data Analysis, scalar data, simplification, feature extraction.

Abstract

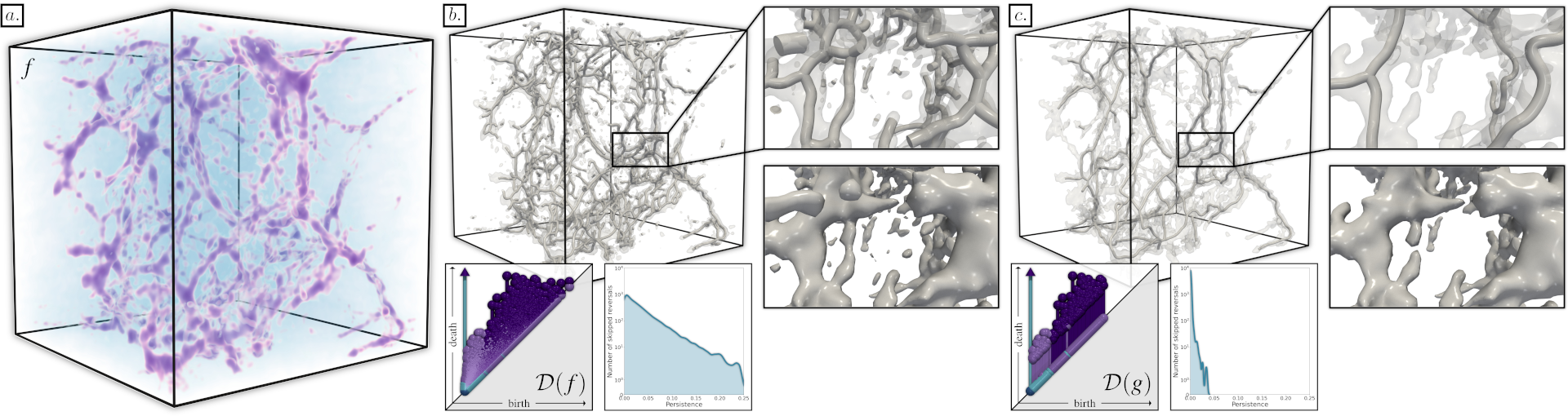
This paper presents a practical approach for the optimization of topological simplification, a central pre-processing step for the analysis and visualization of scalar data. Given an input scalar field f and a set of “signal” persistence pairs to maintain, our approaches produces an output field g that is close to f and which optimizes (i) the cancellation of “non-signal” pairs, while (ii) preserving the “signal” pairs. In contrast to pre-existing simplification approaches, our method is not restricted to persistence pairs involving extrema and can thus address a larger class of topological features, in particular saddle pairs in three-dimensional scalar data. Our approach leverages recent generic persistence optimization frameworks and extends them with tailored accelerations specific to the problem of topological simplification. Extensive experiments report substantial accelerations over these frameworks, thereby making topological simplification optimization practical for real-life datasets. Our work enables a direct visualization and analysis of the topologically simplified data, e.g., via isosurfaces of simplified topology (fewer components and handles). We apply our approach to the extraction of prominent filament structures in three-dimensional data. Specifically, we show that our pre-simplification of the data leads to practical improvements over standard topological techniques for removing filament loops. We also show how our framework can be used to repair genus defects in surface processing. Finally, we provide a C++ implementation for reproducibility purposes.