Out-of-Core Dimensionality Reduction for Large Data via Out-of-Sample Extensions

Fast forward

Abstract

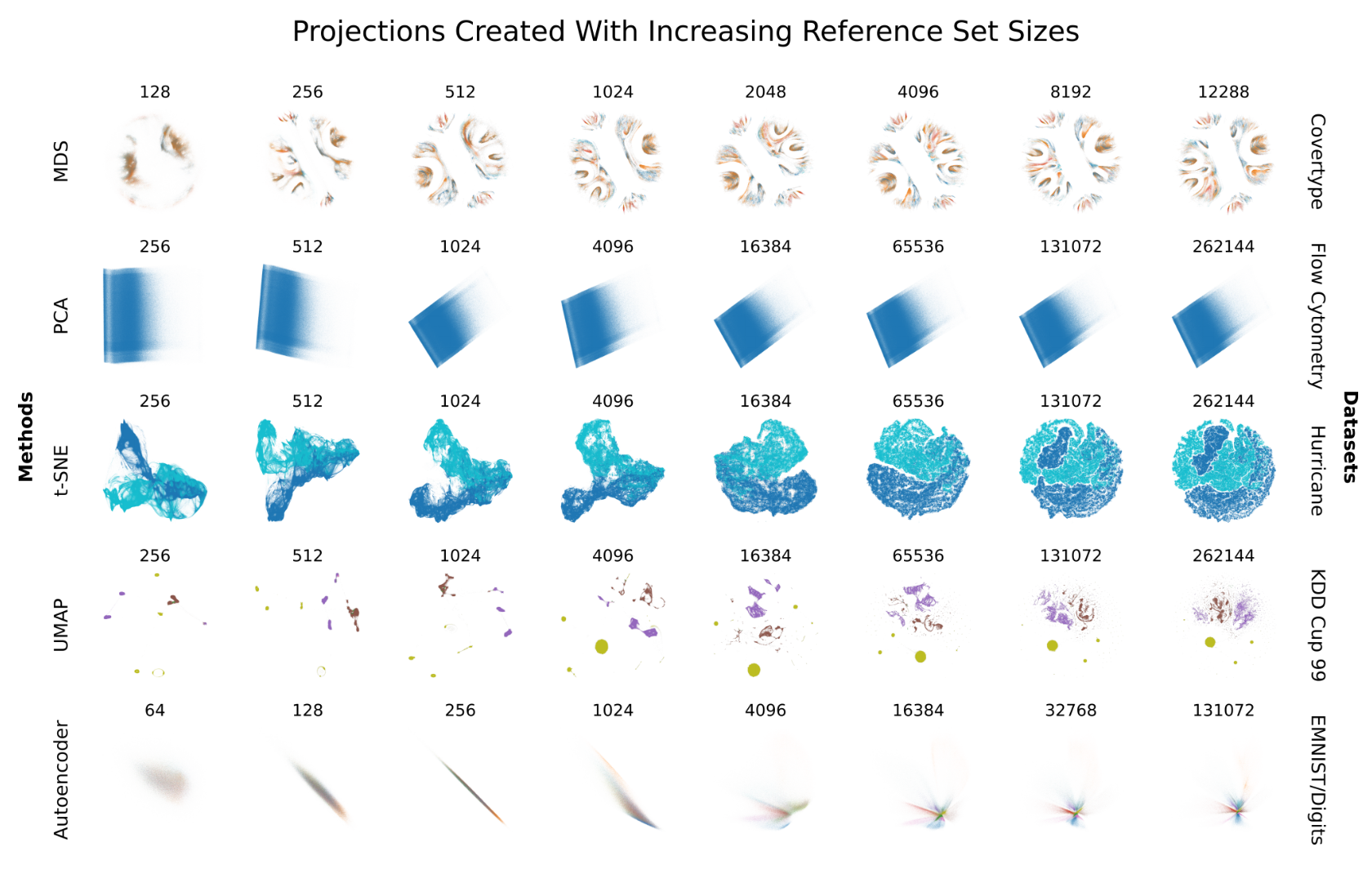
Dimensionality reduction (DR) is a well-established approach for the visualization of high-dimensional data sets. While DR methods are often applied to typical DR benchmark data sets in the literature, they might suffer from high runtime complexity and memory requirements, making them unsuitable for large data visualization especially in environments outside of high-performance computing. To perform DR on large data sets, we propose the use of out-of-sample extensions.Such extensions allow inserting new data into existing projections, which we leverage to iteratively project data into a reference projection that consists only of a small manageable subset. This process makes it possible to perform DR out-of-core on large data, which would otherwise not be possible due to memory and runtime limitations. For metric multidimensional scaling (MDS), we contribute an implementation with out-of-sample projection capability since typical software libraries do not support it. We provide an evaluation of the projection quality of five common DR algorithms (MDS, PCA, t-SNE, UMAP, and autoencoders) using quality metrics from the literature and analyze the trade-off between the size of the reference set and projection quality. The runtime behavior of the algorithms is also quantified with respect to reference set size, out-of-sample batch size, and dimensionality of the data sets. Furthermore, we compare the out-of-sample approach to other recently introduced DR methods, such as PaCMAP and TriMAP, which claim to handle larger data sets than traditional approaches. To showcase the usefulness of DR on this large scale, we contribute a use case where we analyze ensembles of streamlines amounting to one billion projected instances.